Recon#
This module allows the user to run pre-configured reconstruction algorithms on their data.
Analytical Reconstruction#
The CIL analytical reconstructions use CIL to filter and prepare the data using highly optimised routines. The filtered data is then backprojected using projectors from TIGRE or ASTRA-TOOLBOX.
Standard FBP (filtered-backprojection) should be used for parallel-beam data. FDK (Feldkamp, Davis, and Kress) is a filtered-backprojection algorithm for reconstruction of cone-beam data measured with a standard circular orbit.
The filter can be set to a predefined function, or a custom filter can be set. The predefined filters take the following forms:
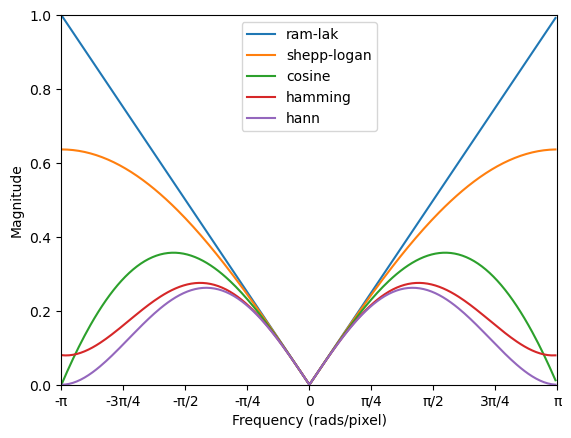
FBP - Reconstructor for parallel-beam geometry#
- class cil.recon.FBP(input, image_geometry=None, filter='ram-lak', backend='tigre')[source]#
Creates an FBP reconstructor based on your parallel-beam acquisition data.
- Parameters:
input (AcquisitionData) – The input data to reconstruct. The reconstructor is set-up based on the geometry of the data.
image_geometry (ImageGeometry, default used if None) – A description of the area/volume to reconstruct
filter (string, numpy.ndarray, default='ram-lak') – The filter to be applied. Can be a string from: {’ram-lak’, ‘shepp-logan’, ‘cosine’, ‘hamming’, ‘hann’}, or a numpy array.
backend (string) – The backend to use, can be ‘astra’ or ‘tigre’. Data must be in the correct order for requested backend.
Example
>>> from cil.utilities.dataexample import SIMULATED_PARALLEL_BEAM_DATA >>> from cil.recon import FBP >>> data = SIMULATED_PARALLEL_BEAM_DATA.get() >>> fbp = FBP(data) >>> out = fbp.run()
Notes
The reconstructor can be further customised using additional ‘set’ methods provided.
- set_split_processing(slices_per_chunk=0)[source]#
Splits the processing in to chunks. Default, 0 will process the data in a single call.
- Parameters:
out (slices_per_chunk, optional) – Process the data in chunks of n slices. It is recommended to use value of power-of-two.
Notes
This will reduce memory use but may increase computation time. It is recommended to tune it too your hardware requirements using 8, 16 or 32 slices.
This can only be used on simple and offset data-geometries.
- run(out=None, verbose=1)[source]#
Runs the configured FBP recon and returns the reconstruction
- Parameters:
out (ImageData, optional) – Fills the referenced ImageData with the reconstructed volume and suppresses the return
verbose (int, default=1) – Controls the verbosity of the reconstructor. 0: No output is logged, 1: Full configuration is logged
- Returns:
The reconstructed volume. Suppressed if out is passed
- Return type:
- get_filter_array()#
Returns the filter array in the frequency domain.
- Returns:
An array containing the filter values
- Return type:
numpy.ndarray
Notes
The filter length N is 2^self.fft_order.
The indices of the array are interpreted as:
[0] The DC frequency component
[1:N/2] positive frequencies
[N/2:N-1] negative frequencies
The array can be modified and passed back using set_filter()
Notes
Filter reference in frequency domain: Eq. 1.12 - 1.15 T. M. Buzug. Computed Tomography: From Photon Statistics to Modern Cone-Beam CT. Berlin: Springer, 2008.
Plantagie, L. Algebraic filters for filtered backprojection, 2017 https://hdl.handle.net/1887/48289
- plot_filter()#
Returns a plot of the filter array.
Requires matplotlib-base (or matplotlib) to be installed.
- Returns:
A plot of the filter
- Return type:
matplotlib.pyplot
- set_fft_order(order=None)#
The width of the fourier transform N=2^order.
- Parameters:
order (int, optional) – The width of the fft N=2^order
Notes
If None the default used is the power-of-2 greater than 2 * detector width, or 8, whichever is greater Higher orders will yield more accurate results but increase computation time.
- set_filter(filter='ram-lak', cutoff=1.0)#
Set the filter used by the reconstruction.
Pre-set filters are constructed in the frequency domain. Pre-set filters are: ‘ram-lak’, ‘shepp-logan’, ‘cosine’, ‘hamming’, ‘hann’
- Parameters:
filter (string, numpy.ndarray, default='ram-lak') – Pass a string selecting from the list of pre-set filters, or pass a numpy.ndarray with a custom filter.
cutoff (float, default = 1) – The cut-off frequency of the filter between 0 - 1 pi rads/pixel. The filter will be 0 outside the range rect(-frequency_cutoff, frequency_cutoff)
Notes
If passed a numpy array the filter must have length N = 2^self.fft_order
The indices of the array are interpreted as:
[0] The DC frequency component
[1:N/2] positive frequencies
[N/2:N-1] negative frequencies
- set_filter_inplace(inplace=False)#
False (default) will allocate temporary memory for filtered projections. True will filter projections in-place.
- Parameters:
inplace (boolean) – Sets the inplace filtering of projections
- set_image_geometry(image_geometry=None)#
Sets a custom image geometry to be used by the reconstructor
- Parameters:
image_geometry (ImageGeometry, default used if None) – A description of the area/volume to reconstruct
- set_input(input)#
Update the input data to run the reconstructor on. The geometry of the dataset must be compatible with the reconstructor.
- Parameters:
input (AcquisitionData) – A dataset with a compatible geometry
FDK - Reconstructor for cone-beam geometry#
- class cil.recon.FDK(input, image_geometry=None, filter='ram-lak')[source]#
Creates an FDK reconstructor based on your cone-beam acquisition data using TIGRE as a backend.
- Parameters:
input (AcquisitionData) – The input data to reconstruct. The reconstructor is set-up based on the geometry of the data.
image_geometry (ImageGeometry, default used if None) – A description of the area/volume to reconstruct
filter (string, numpy.ndarray, default='ram-lak') – The filter to be applied. Can be a string from: {’ram-lak’, ‘shepp-logan’, ‘cosine’, ‘hamming’, ‘hann’}, or a numpy array.
Example
>>> from cil.utilities.dataexample import SIMULATED_CONE_BEAM_DATA >>> from cil.recon import FDK >>> data = SIMULATED_CONE_BEAM_DATA.get() >>> fdk = FDK(data) >>> out = fdk.run()
Notes
The reconstructor can be futher customised using additional ‘set’ methods provided.
- run(out=None, verbose=1)[source]#
Runs the configured FDK recon and returns the reconstruction.
- Parameters:
out (ImageData, optional) – Fills the referenced ImageData with the reconstructed volume and suppresses the return
verbose (int, default=1) – Controls the verbosity of the reconstructor. 0: No output is logged, 1: Full configuration is logged
- Returns:
The reconstructed volume. Suppressed if out is passed
- Return type:
- get_filter_array()#
Returns the filter array in the frequency domain.
- Returns:
An array containing the filter values
- Return type:
numpy.ndarray
Notes
The filter length N is 2^self.fft_order.
The indices of the array are interpreted as:
[0] The DC frequency component
[1:N/2] positive frequencies
[N/2:N-1] negative frequencies
The array can be modified and passed back using set_filter()
Notes
Filter reference in frequency domain: Eq. 1.12 - 1.15 T. M. Buzug. Computed Tomography: From Photon Statistics to Modern Cone-Beam CT. Berlin: Springer, 2008.
Plantagie, L. Algebraic filters for filtered backprojection, 2017 https://hdl.handle.net/1887/48289
- plot_filter()#
Returns a plot of the filter array.
Requires matplotlib-base (or matplotlib) to be installed.
- Returns:
A plot of the filter
- Return type:
matplotlib.pyplot
- reset()#
Resets all optional configuration parameters to their default values
- set_fft_order(order=None)#
The width of the fourier transform N=2^order.
- Parameters:
order (int, optional) – The width of the fft N=2^order
Notes
If None the default used is the power-of-2 greater than 2 * detector width, or 8, whichever is greater Higher orders will yield more accurate results but increase computation time.
- set_filter(filter='ram-lak', cutoff=1.0)#
Set the filter used by the reconstruction.
Pre-set filters are constructed in the frequency domain. Pre-set filters are: ‘ram-lak’, ‘shepp-logan’, ‘cosine’, ‘hamming’, ‘hann’
- Parameters:
filter (string, numpy.ndarray, default='ram-lak') – Pass a string selecting from the list of pre-set filters, or pass a numpy.ndarray with a custom filter.
cutoff (float, default = 1) – The cut-off frequency of the filter between 0 - 1 pi rads/pixel. The filter will be 0 outside the range rect(-frequency_cutoff, frequency_cutoff)
Notes
If passed a numpy array the filter must have length N = 2^self.fft_order
The indices of the array are interpreted as:
[0] The DC frequency component
[1:N/2] positive frequencies
[N/2:N-1] negative frequencies
- set_filter_inplace(inplace=False)#
False (default) will allocate temporary memory for filtered projections. True will filter projections in-place.
- Parameters:
inplace (boolean) – Sets the inplace filtering of projections
- set_image_geometry(image_geometry=None)#
Sets a custom image geometry to be used by the reconstructor
- Parameters:
image_geometry (ImageGeometry, default used if None) – A description of the area/volume to reconstruct
- set_input(input)#
Update the input data to run the reconstructor on. The geometry of the dataset must be compatible with the reconstructor.
- Parameters:
input (AcquisitionData) – A dataset with a compatible geometry